Deep LPF:Deep Local Parametric Filters for Image Enhancement

23 Jun 2021

Reading time ~9 minutes

Deep LPF:Deep Local Parametric Filters for Image Enhancement

Deep LPF:Deep Local Parametric Filters for Image Enhancement 는 local parameter filter의 학습을 통해 image enhancement를 수행하는 방법에 관한 논문입니다.

논문 주소 : https://arxiv.org/abs/2003.13985
코드 깃허브 : https://github.com/sjmoran/DeepLPF

Introduction

디지털 카메라와 센서, 그리고 사진의 성능 향상은 최근 몇년간 급격한 성장을 이루었습니다. 하지만 여전히 촬영 기법이나 기계의 문제로 사진에 보정이 필요한 경우가 많습니다.

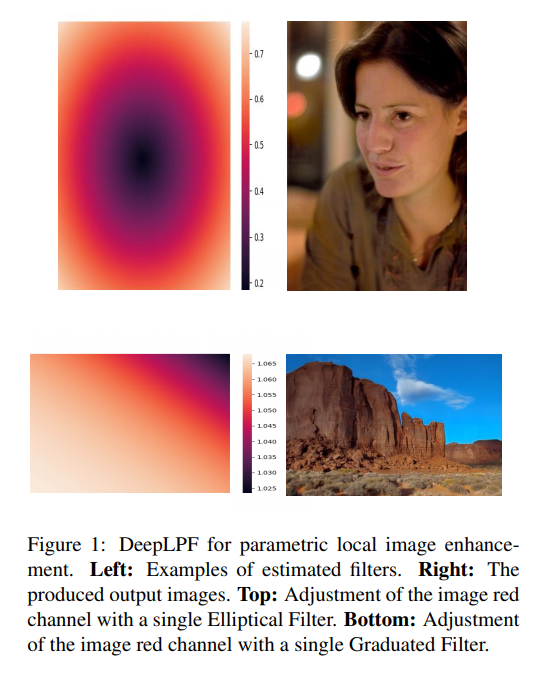
lpf_fig1

단순하게 밝기나 대비를 전체적으로 조정하는 것은 쉽지만 fig1에 나온것처럼, 지역적인 영상을 수동적으로 조정하는 것은 비전문가에게는 어려운 일입니다. 이러한 문제를 해결하기 위해 비전문가도 전문가처럼 local filter들을 이용하여 이미지 향상을 수행할 수 있는 방법을 제시합니다. DeepLPF에서는 deep neural network를 이용하여 local editing tool들을 모델링하고, 에뮬레이션합니다. 주어진 input, enhanced의 training example들을 통해 local, mid-level의 조정을 수행할 수 있는 graduated and elliptical filter들에 대해 학습합니다. 이렇게 디지털 아티스트가 사용하는 도구와 유사한 도구를 활용하는 방법을 배우는 모델을 통해 자연스러운 형태의 정규화된 모델을 제공하며, 자연스러운 모델 정규화 및 직관적인 조정이 가능하도록 합니다. 이에 대한 내용을 정리하면 다음과 같습니다.

Local Parametric Filters : DeepLPF에서는 local image enhancement를 위한 자동 평가 parametric filter 들을 사용합니다. 여기서 사용되는 필터의 종류는 3가지로 각각, 타원형 필터(Elliptical filter), 그라데이션 필터(Graduated filter), 다항식 필터(Polynomial filter)입니다. 여기서 제공하는 공식들은 직관적으로 해석 가능하고, 본질적으로 규칙화된 필터들을 만들어냄으로써, 가중치 효율성(weight efficiency)과 overfitting 현상을 방지합니다.
Multiple Filter Fusion Block : 이 논문에서는 여러 파라미터 이미지 필터들을 결합하기 위한 블록을 제시합니다. 이 plug-and-play 형태의 블록들은 다수의 독립된 파라미터 필터들의 결과물들을 결합하며, 이미지 퀄리티 향승을 위한 보통의 backbone network와 결합할 수 있는 유연한 레이어를 제공합니다.
SOTA Image Enhancement Quality : DeepLPF는 SOTA 수준의 이미지 향상 능력을 2개의 benchmark에서 보여줍니다.

디지털 사진 개선은 오래전부터 연구되어오던 분야입니다. 기존의 이미지 개선 연구들은 크게 몇 가지 방법들로 구분할 수 있는데, globally 혹은 locally, 그리고 둘 모두를 사용한 방법들이 있습니다.

Global Image Enhancement
Local image Enhancement
Global and Local Image Enhancement

Deep Local Parametric Filters

lpf_fig2

DeepLPF는 local image enhancement를 위한 방식을 정의하는데, 유사한 수동 필터의 결합 어플리케이션 과정을 따라할 수 있도록 디자인된 로컬 파라메트릭 이미지 펄터들의 출력을 결합하여 결과를 뽑는 딥 퓨전 아키텍처를 도입합니다. 이 논문에서는 가장 많이 사용되는 3가지 필터인 타원형 필터(Elliptical filter), 그라데이션 필터(Graduated filter), 다항식 필터(Polynomial filter)를 인스턴스화합니다. 각 필터에 대한 예시로, Fig2 는 각 Lightroom filter들이 어떻게 사용되는지 비교하여 보여줍니다. Section 3.1에서는 다른 집합의 파라메트릭 필터를 학습하도록 설계된 DeepLPF의 전체적인 구조를 설명하고, Section 3.2에서는 3개의 로컬 파라메트릭 필터에 대한 설명을, 마지막으로 Section 3.3과 3.4에서는 어떻게 여러개의 filter들이 하나로 융합되는지와 학습을 어떻게 수행했는지에 대해 설명합니다.

3.1 Deep LPF Architecture

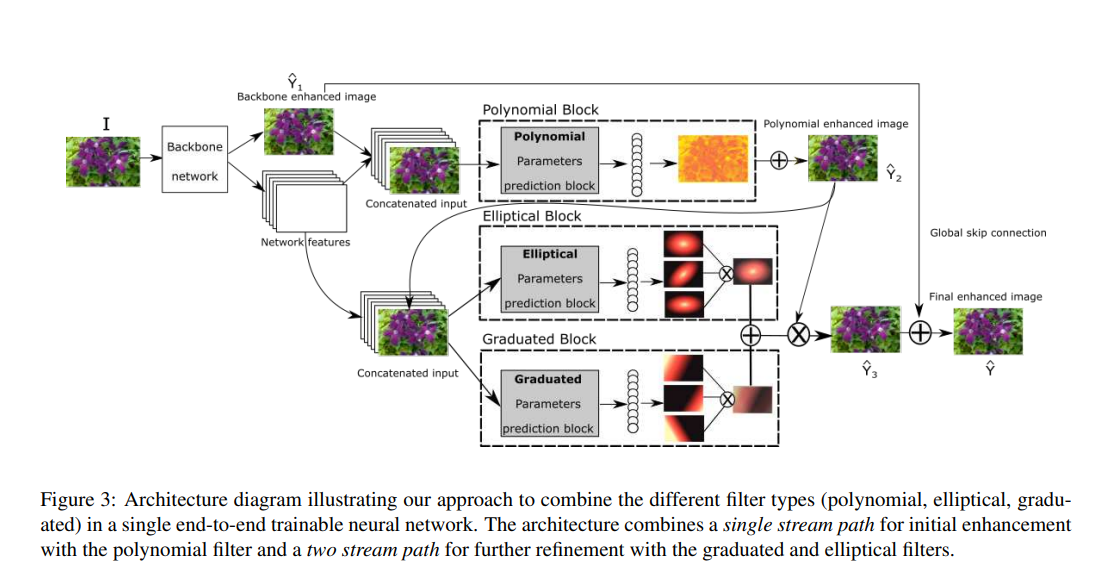
lpf_fig3

DeepLPF의 구조는 Figure 3에 나온 것과 같습니다. 저화질의 입력 이미지 $I$와 변환 목표로 삼는 고화질의 이미지 $Y$가 존재한다고 할 때, DeepLPF는 변환 함수 $f_\theta$를 $Y$에 가까운 값인 $\hat{Y}=f_\theta (I)$을 정의하도록 학습하는 구조가 됩니다. 이 모델은 단일-스트림 네트워크 구조를 세밀한 향상을 위해 사용하고, 보다 높은 수준의 지역 향상(local enhancement)을 위해 이중-스트림 구조를 사용합니다. 이 논문에서는 먼저 표준 CNN backbone (ResNet이나 Unet과 같은)을 $H\times W \times C$차원의 특징맵(feature map)으로 변환하는데 사용합니다. 특징맵의 첫 3개의 channel들은 조정할 이미지를 나타내며, 나머지 $C’ = C-3$ 개의 채널들은 세개의 필터 파라미터 예측 블록에 공급되는 추가 feature들을 의미합니다. 첫 단일-스트림 통로는 backbone에서 향상된 입력 이미지의 픽셀들에 적용되는 다항식 필터(Polynomial filter)의 파라미터를 추정합니다. 이 블록은 브러쉬의 모양에 따라 부드러움이 제한되며, 이미지들의 pixel level에서 영상을 조정하는 브러쉬 도구를 모방합니다. 이렇게 다항식 필터(polynomial filter)를 통해 향상된 이미지 $\hat{Y}_2$는 $C’$ backbone feature와 합쳐지고, 좀더 제한적으로 이중-스트림 통로의 입력으로 사용됩니다. 타원형 필터(elliptical filter)와 그라데이션 필터(graduated filter)의 조정 맵 같은 경우에는 두 개의 평행한 회귀 블록(regression blocks)에 의해 추정됩니다. 타원형 필터와 그라데이션 필터의 특징맵은 단순 덧셈을 통해 융합됩니다. 다만 이때, 가중 조합(weighted combination)과 같은 다른 방법을 사용해도 됩니다. 이러한 융합과정은 스케일링 맵 $\hat{S}$ 에 $\hat{Y}_2$에 element-wise multiplied 되어 이미지 $\hat{Y}_3$ 을 제공하고, 타원형, 그라데이션 조정을 다항식 필터로 인해 향상된 이미지에 효과적으로 적용하게 됩니다. 백본 네트워크를 통해 향상된 이미지 $\hat{Y}_1$ 은 최종적으로 긴 residual connection을 통해 $\hat{Y}_3$에 더해지고, 최종적으로 향상된 결과 이미지 $\hat{Y}$가 나오게 됩니다.

3.2 Local Parametric Filters

앞서 3개의 local parametric filter 예시를 설명했는데, 각 필터는 파라미터 형태에 따라 다른 타입의 이미지 조정을 수행하며, 파라미터 값이 각 경웨 정확한 임지 효과를 지정합니다. 필터 파라미터 값들은 이미지마다 다르며 supervised CNN regression에 의해 예측됩니다.(3.2.1)

Filter Parameter Prediction Network(3.2.1)

DeepLPF의 파라미터 예측 블록(parameter prediction block)은 백본 네트워크와 회귀 필터 파라미터들에서 특징 집합(feature set)을 받아들이는 가벼운 CNN 구조입니다. 이 네트워크 블록은 컨볼루션 레이어와 맥스 풀링 레이어 세트의 downsampling 역할을 대체합니다. 그 다음 레이어들에는 필터 파라미터 예측을 위한 GAP 레이어와 FC 레이어가 존재합니다. GAP 레이어는 네트워크가 입력 특징세트와 무관하게 해상도가 유지되도록 합니다. 활성화함수(activation function)으로는 Leaky ReLU와 dropout을 FC layer에 적용하였습니다.

예시로 든 3가지 필터의 경우, 회귀 네트워크들 간의 유일한 차이점은 FC 레이어의 출력 노드 수 뿐입니다. 이는 해당 필터를 정의하는 파라미터 수에 해당합니다.(Table 1.)

lpf_table1

최근의 로컬 픽셀 수준의 이미지 향상 방법들과 비교했을 때, 학습에 필요한 파라미터의 수가 크게 줄어든 것입니다. DeepLPF 네트워크의 output size는 동일한 필터 타입의 다양한 인스턴스의 파라미터를 예측하기 위해서 대체될 수 있습니다. 논문의 저자는 이미지 변환에 필요한 파라미터의 예측 방법이 파리머터화한 이미지 변환이 직접적인 이미지 변환보다 효과적이라는 지난 연구와 이어진다고 말합니다. 중요한 점은, 회귀 네트워크(regression network)가 백본 모델과 무관하게 이미지 필터를 통해 영상변환네트워크(image translation netwrok)의 향상에 도움이 된다는 것입니다.

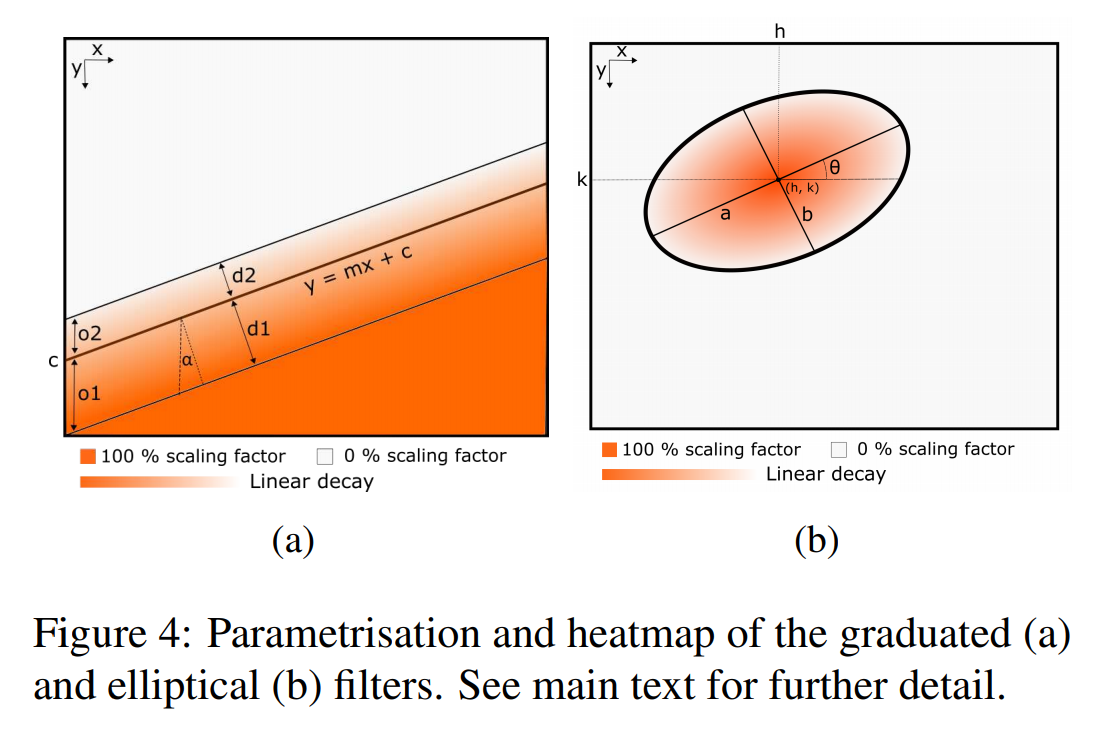
lpf_fig4.a

Graduated Filter(3.2.2)

그라데이션 필터(Graduated filter) 는 일반적으로 사진 편집 프로그램에서 이미지의 고대비(high contrast) 평면 영역(과노출이 발생한 하늘처럼)을 조정하는 데 사용됩니다. 이 논문에서 구현한 그라데이션 필터는 Fig 4.a에 묘사되어있습니다.

이 그라데이션 필터는 3개의 평행선을 따라서 정의되며, 가운데 선은 filter의 위치와 방향(orientation)을 결정하며 $y=xm+c$의 형태로 정의됩니다. Offset $o1$과 $o2$는 각 adjustmap이 heatmap $s(x,y)$를 형성하는 4개의 서로 다른 영역으로 구성되도록 하는 2개의 추가 파라미터를 제공합니다. 100% 영역의 모든 픽셀들에 대해 스케일링 파라미터 $s_g$를 곱하고, 100-50% 영역에 대해서는 선형적으로 $s_g$에서 $\frac{s_g}{2}$ 까지 감소한 파라미터를 곱해주며, 마지막으로 50-0% 영역의 스케일링 값은 픽셀들이 조정되지 않은 0% 영역에 도달할때까지 선형적으로 감소합니다. 수학적으로 그라데이션 필터를 표현하면 다음 방정식이 됩니다.

\[a(x,y)=s_gmin\left\{ { { \frac {1} {2} } ( { 1 + { \frac { \ell (x,y) }{d_2} } } ) , 1 } \right\} (1)\] \[b(x,y)=s_gmax\left\{ { { \frac {1} {2} } ( { 1 + { \frac { \ell (x,y) } {d_1} } } ), 0} \right\} (2)\] \[f(n)=\begin{cases}{\hat{g}_{inv}}a(x,y)+(1-{\hat{g}_{inv}})b(x,y) & ,l(x,y)\ge0 \\(1-{\hat{g}_{inv}})a(x,y)+{\hat{g}_{inv}}b(x,y) &,l(x,y) <0 \end{cases}\]

$\ell(x,y)=y-(mx+c)$는 중심선에 상대적인 점 $(x,y)$의 위치 함수이고, $d_1=o_1 cos\alpha$, $d_2=o_2cos\alpha$, $\alpha=tan^{-1}$이며, $\hat{g}_{inv}$는 이항 지시 변수(binary indicator variable)입니다. 파라미터 $\hat{g}_{inv}$는 상단과 하단 라인에 대한 inversion이 가능하도록 합니다. inversion은 중심선에 대한 100% 스케일링 영역의 위치를 결정합니다. inversion을 학습할 수 있도록 하기 위해서, 모델은 binary indicator parameter $\hat{g}_{inv}={\frac{1}{2}}(sgn(g_{inv})+1)$을 예측하는데, 여기서 $sgn$은 sign function을 나타내고, $g_{inv}$는 실제 값으로 예측된 파라미터를 의미하며 ${\hat{g}_{inv}}$는 ${\hat{g}_{inv}} \in \left\{0,1\right\}$ 으로 이진화된 버전을 말합니다. sign function의 기울기값은 모든 곳에서 0이고, 0에서 정의되지 않으므로, 이 이진 변수를 학습하기 위해 backward pss의 straight-through estimator를 사용합니다.

Elliptical Filter (3.2.3)

타원형의 추가 필터는 center $(h,k)$, 반장축(semi-major axis) $(a)$, 반단축(semi-minor axis) $(b)$ 그리고 회전각(rotation angle) $(\theta)$ 의 파라미터로 정의됩니다. 학습된 스케일링 팩터 $s_e$는 타원의 중심(100% point)을 최대화 하고, 경계에 도달할 때까지 선형적으로 감소합니다. 픽셀들은 타원 밖에서는 조정되지 않습니다.(0% 영역) 수학적으로 타원형 필터에 의해 정의되는 channel-wise heatmap은 다음을 통해 정의됩니다.

\[s(x,y)=s_emin \left(0,1- \frac{[(x-h)cos\theta + (y-k)sin\theta]^2}{a^2} +\frac {[(x-h)sin\theta + (y-k)cos\theta}{b^2 } \right)\]

예시로 생성한 타원형 필터의 모습과 히트맵은 fig 4.(b)에 나와있습니다. 타원형 필터는 사진에서 주목할만한 물체나 특정 지역(사람 얼굴 등)을 향상시키는 데에 사용됩니다.

Polynomial Filter (3.2.4)

세 번째 필터는 다항식 필터입니다. 다항식 필터는 전체 이미지에 대해 세분화되고, 규칙적인 조정을 수행합니다. 다항식 필터는 브러쉬 도구를 참고하여 만들어졌는데, 브러쉬 툴의 공간을 매끄럽게 하는 넓은 범위의 도형을 제공하는 기능을 모방합니다. 논문에서는 p-번째(order-p)의 다항식 필터의 식을 $i \cdot (x+y+\gamma)^p$ 와 $(x+y+i+\gamma)^p$로 정하는데, 이 때 $i$는 이미지의 $(x,y)$ 위치의 이미지 채널 강도(image channel intensity)를 의미하고, $\gamma$는 독립적인 스칼라 값을 나타냅니다. 논문에서는 경험적으로 정육면체 다항식(cubic polynomial, $p=3$)이 표현적 이미지 조정을 제공하면서도 제한된 매개변수 집합만을 제공한다는 것을 확인하였고, cubic-10, cubic-20의 2가지 cubic filter를 실험하였습니다.

작은 cubic filter(cubic-10)의 경우에는 10개의 예측해야할 파라미터로 이루어져 있습니다. $f$로 정의된 cubic function 은 intensity $i$를 새롭게 조정된 intensity $i’%$로 바꾸어주는 함수이며, 다음과 같이 정의됩니다.

\[\begin{matrix} i'(x,y) &=& f(x,y,i) \\&=&i*(Ax^3+Bx^2y+Cx^2+D+ \\&&+Dx^2+Exy+Fx+Gy^3+Hy^2 \\ &&+Iy+J) \end{matrix}\]

이에 비해 2배의 학습 가능한 파라미터를 갖고 있는 cubic-20 필터는 더 고차원의 intensity terms들을 탐색하고 20개의 파라미터 집합으로 표현됩니다.

\[\begin{matrix} i'(x,y) &=& f(x,y,i) \\&=&i*(Ax^3+Bx^2y+Cx^2i+Dx^2+Exy^2 \\&&+Fxyi+Gxy+Hxi^2+Ixi+Jx \\&& +Ky^3+Ly^2i+My^2+Nyi^2+Oyi \\&& +Py+Qi^3+Ri^2+Si+T \end{matrix}\]

이러한 큐빅 필터들은 공간과 강도의 정보를 모두 고려하여 학습된 매핑의 복잡성을 정규화된 형태로 제한합니다. 이는 이미지의 변환이 지역적인 매끄러움을 보장하면서도 정교하고, 픽셀 단위의 이미지 향상이 가능하도록 합니다. 여기에 각 색상 채널에 대해 독립적인 cubic function을 추정하여 cubic-10에는 30개의 파라미터를 정하고, cubic-20에는 60개의 파라미터를 산출합니다.

lpf_fig5

3.3 Fusing Multiple Filters of the Same Type

그라데이션 및 타원형 블록은 해당 필터 유형의 n개의 인스턴스에 대하여 각 출력 파라미터 값을 사용할 수 있습니다. 이 때 n을 적절하게 선택할 수 있는 방법에 대한 추가적인 연구는 4.2절에 자세하게 설명되어 있습니다. $n > 1$인 경우, 여러 인스턴스들은 요소별 곱셈(element-wise multiplication)을 통해 조정 맵(adjustment map)에 결합됩니다. 이 곱셈은 다음과 같이 표현 할 수 있습니다

\[s_g(x,y) = \prod_{i=1}^n s_{gi}(x,y), s_e(x,y) = \prod_{i=1}^n s_{ei}(x,y)\]

여기서 $s_{gi}(x,y)$ 와 $s_{ei}(x,y)$는 각각 그라데이션 필터와 타원형 필터의 $i$ 번째 인스턴스 조정 맵을 말한다. 이와는 반대로, 단일 채널 당 큐빅 필터는 표현력 측면에서 본질적으로 높은 유연성을 보이기 때문에 여러 개의 큐빅 필터를 융합해서 사용하지는 않습니다.

3.4 DeepLPF Loss Function

DeepLPF의 학습 로스는 CIELab 색공간을 활용하여 $L_1$ 로스를 Lab 채널로 계산하고 MS-SSIM 로스는 L 채널에서 계산합니다. 채도와 광도 정보를 분리하여 loss 들에 다른 정보를 줌으로써, 모델은 local과 global 영역 양쪽 모두에 집중하여 학습되는 동안 이미지 향상을 수행할 수 있게 됩니다. N개의 image pair들 $\left\{ (Y_i,\hat(Y)_i) \right\}_{i=1}^N$ 이 주어질 때($Y_i$는 reference image이고, $\hat{Y}_i$는 predicted image 라고 할 때), DeepLPF의 loss fucntion은 다음과 같이 정의됩니다.

\[\mathcal{L} = \sum_{i=1}^{N} \left\{ \omega_{lab} \lVert Lab(\hat{Y}_i) - Lab(Y_i) \rVert_1 + \omega_{ms-ssim}MS{\scriptstyle\text{-}}SSIM(L(\hat{Y}_i),L(Y_i))) \right\}\]

여기서 $Lab(\cdot)$은 입력 RGB 이미지를 CIELab 채널로 변환하는 함수이며 $L$은 CIELab 채널 이미지의 L 값을 return하는 함수입니다. MS-SSIM은 여러 스케일에 대한 SSIM 값을 의미합니다. $\omega_{lab}과 \omega_{ms-ssim}$은 하이퍼 파라미터로, loss function의 상대적인 영향을 조정할 수 있습니다.

Experiments

Datasets: DeepLPF는 2개의 유명한 데이터셋을 이용하여 테스트되었습니다. 먼저 MIT-Adobe-5K-DPE는 2250장을 train, 2250장을 validation 으로, 500장을 test로 사용하는 방식입니다. DPE에서 사용된 방식으로 Adobe 5k dataset을 분할하여 테스트하는 방법 중 하나입니다 MIT-Adobe-5K-UPE는 이와는 조금 다르게 4500장을 train, 500장을 test로 사용하여 학습하는 방식입니다.

두 번째로 사용한 dataset은 SID(See-in-Dark) Dataset입니다. 이 데이터셋은 5094개의 이미지를 갖고 있으며, 단노출으로 촬영한 input image와 장노출으로 촬영한 label image를 이용하여 학습을 수행하는 것입니다.

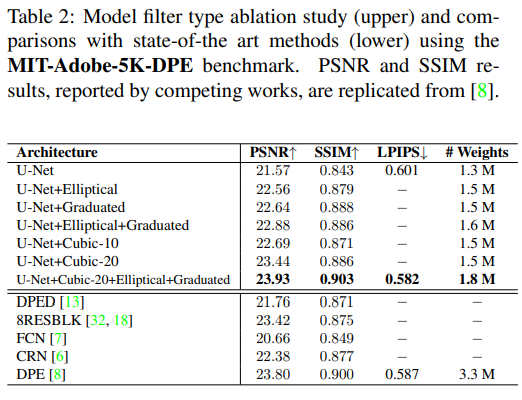
lpf_table2

비교를 위해 선택한 기준은 PSNR, SSIM, LPIPS입니다. 실험 결과는 table 2에 정리되어 있는데, Adobe5k-DPE 를 기준으로 테스트한 결과를 나타냅니다. 가장 먼저 기본적인 U-Net 구조와 U-Net 구조를 backbone으로 하고 각 filter들을 적용한 결과들을 순차적으로 보여줍니다 이 중 U-Net을 backbone으로 하고, cubic-20 filter와 타원형, 그라데이션 필터를 적용한 모델이 가장 좋은 성능을 보였습니다.

lpf_fig7

위 사진들은 비교하는 Method들과 DeepLPF의 결과물 차이를 보여줍니다.

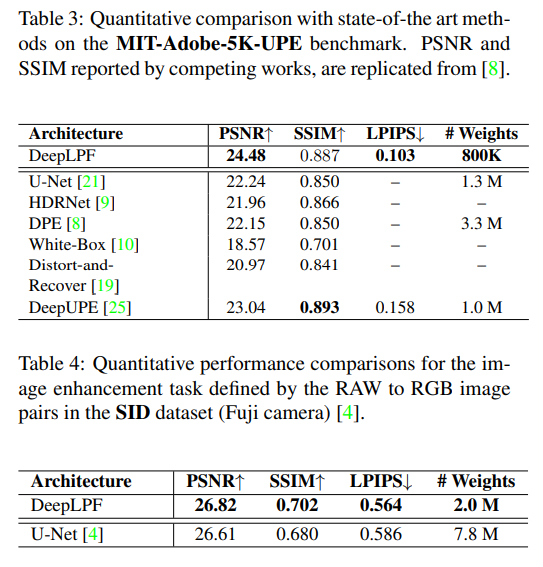
lpf_table3_4

table 3에서는 adobe5k dataset의 deep-upe 방식으로 학습 및 테스트한 결과에 대한 자료이고, table4는 SID Dataset에 대한 결과를 보여줍니다.